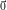 ≠f⊥
w{f1,f2,…,fk-1}Dw(f), and a
certain non-zero vector fk attains the minimum.
≠f⊥
w{f1,f2,…,fk-1}Dw(f), and a
certain non-zero vector fk attains the minimum.
In our examples, we need to verify that we have the correct value for γk := min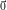 ≠f⊥
w{f1,f2,…,fk-1}Dw(f), and a
certain non-zero vector fk attains the minimum.
≠f⊥
w{f1,f2,…,fk-1}Dw(f), and a
certain non-zero vector fk attains the minimum.
The first step is straightforward, and we check that fk is perpendicular to {f1,…,fk-1} in the weighted space, and Dw(fk) equals γk.
The second step is to check that for all 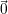 ≠f ⊥w{f1,f2,…,fk-1}, Dw(f) ≥ γk. As the numerator in the definition
of Dw(f) involves the maximum operator, we use a program to consider all cases of the relative order of the nodes
with respect to f.
≠f ⊥w{f1,f2,…,fk-1}, Dw(f) ≥ γk. As the numerator in the definition
of Dw(f) involves the maximum operator, we use a program to consider all cases of the relative order of the nodes
with respect to f.
For each permutation σ : [n] → V , for e ∈ E, we define Sσ(e) := σ(max{i : σ(i) ∈ e}) and Iσ(e) := σ(min{i : σ(i) ∈ e}).
We consider the mathematical program P(σ) := min∑ e∈Ewe ⋅ (f(Sσ(e)) - f(Iσ(e)))2 - γk ⋅∑ u∈V wuf(u)2 subject to f(σ(n)) ≥ f(σ(n - 1)) ≥ ⋅⋅⋅ f(σ(1)) and ∀i ∈ [k - 1],$\langle$fi, f$\rangle$ = 0. Since the objective function is a polynomial, and all constraints are linear, the Mathematica function Minimize can solve the program.
Moreover, the following two statements are equivalent.
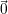 ≠f ⊥w{f1,f2,…,fk-1}, Dw(f) ≥ γk.
≠f ⊥w{f1,f2,…,fk-1}, Dw(f) ≥ γk.
Hence, to verify the first statement, it suffices to use Mathematica to solve P(σ) for all permutations σ. The test is passed if the total number of violations is zero.
Consider the following hypergraph with 5 vertices and 5 hyperedges each with unit weight.
We can verify that different minimizers for γ2 lead to different values for γ3.
| i | γi | fiT | γi′ | fi′T |
| 1 | 0 | (1,1,1,1,1) | 0 | (1,1,1,1,1) |
| 2 | 5/6 | (1,1,1,-4,-4) | 5/6 | (2,2,-3,-3,-3) |
| 3 | 113/99 | (2,2,-6,3,-6) | 181/165 | (4,-5,-5,5,5) |
The following code verifies γ2 and γ3.
violation=0;
Fun[list_, mask_] := Module[{ans},
l = Length[mask];
max = 0;
min = l;
Do[
max = Max[Extract[Extract[Position[list, Extract[mask, i]], 1], 1], max];
min = Min[Extract[Extract[Position[list, Extract[mask, i]], 1], 1], min];
, {i, l}];
ans = (Extract[list, max] - Extract[list, min])^2
]
constrain = {m1<=m2, m2<=m3, m3<=m4, m4<=m5, m5==1, 5*a+4*b+3*c+2*d+e==0};
var = {a,b,c,d,e};
Do[
thisObj = Fun[p,{a,b}]+Fun[p,{a,b,c}]+Fun[p,{a,b,c,d}]+Fun[p,{a,b,c,d,e}] - 5/6*(5*a^2+4*b^2+3*c^2+2*d^2+e^2);
thisConstrain = constrain /. {m1 -> Extract[p, {1}], m2 -> Extract[p, {2}], m3 -> Extract[p, {3}],
m4 -> Extract[p, {4}], m5 -> Extract[p, {5}]};
{opt, assign} = Minimize[thisObj, thisConstrain, var];
If[opt<0, violation++, ];
Print["opt=", opt, " perm=", p, " assign=", assign, " obj=", thisObj],
{p, Permutations[{a,b,c,d,e}]}
]
constrain = {m1<=m2, m2<=m3, m3<=m4, m4<=m5, m5==1, 5*a+4*b+3*c+2*d+e==0, 5*a+4*b+3*c-8*d-4*e==0};
var = {a,b,c,d,e};
Do[
thisObj = Fun[p,{a,b}]+Fun[p,{a,b,c}]+Fun[p,{a,b,c,d}]+Fun[p,{a,b,c,d,e}] - 113/99*(5*a^2+4*b^2+3*c^2+2*d^2+e^2);
thisConstrain = constrain /. {m1 -> Extract[p, {1}], m2 -> Extract[p, {2}], m3 -> Extract[p, {3}],
m4 -> Extract[p, {4}], m5 -> Extract[p, {5}]};
{opt, assign}=Minimize[thisObj, thisConstrain, var];
If[opt<0, violation++, ];
Print["opt=", opt, " perm=", p, " assign=", assign, " obj=", thisObj],
{p, Permutations[{a,b,c,d,e}]}
]
constrain={m1<=m2, m2<=m3, m3<=m4, m4<=m5, m5==1, 5*a+4*b+3*c+2*d+e==0, 10*a+8*b-9*c-6*d-3*e==0};
var={a,b,c,d,e};
Do[
thisObj = Fun[p,{a,b}]+Fun[p,{a,b,c}]+Fun[p,{a,b,c,d}]+Fun[p,{a,b,c,d,e}] - 181/165*(5*a^2+4*b^2+3*c^2+2*d^2+e^2);
thisConstrain = constrain /. {m1 -> Extract[p, {1}], m2 -> Extract[p, {2}], m3 -> Extract[p, {3}],
m4 -> Extract[p, {4}], m5 -> Extract[p, {5}]};
{opt, assign}=Minimize[thisObj, thisConstrain, var];
If[opt<0, violation++, ];
Print["opt=", opt, " perm=", p, " assign=", assign, " obj=", thisObj],
{p, Permutations[{a,b,c,d,e}]}
]
Print["Total number of violations =", violation];
Consider the following hypergraph H = (V,E) with V = {a,b,c,d} and E = {ei : i ∈ [5]}. For i≠3, edge ei has weight 1, and edge e3 has weight 2. Observe that every node has weight 3.
We can verify that γ2 = 2/3 by the following code.
violation = 0;
Fun[list_, mask_] := Module[{ans},
l = Length[mask];
max = 0;
min = l;
Do[
max = Max[Extract[Extract[Position[list, Extract[mask, i]], 1], 1], max];
min = Min[Extract[Extract[Position[list, Extract[mask, i]], 1], 1], min];
, {i, l}];
ans = (Extract[list, max] - Extract[list, min])^2
]
obj =
constrain = {m1<=m2, m2<=m3, m3<=m4, m4==1, a+b+c+d==0};
var = {a,b,c,d};
Do[
thisObj = Fun[p,{a,b,c}]+(a-b)^2+(b-d)^2+2*(c-d)^2 - (2/3)*3*(a^2+b^2+c^2+d^2);
thisConstrain = constrain /. {m1 -> Extract[p, {1}], m2 -> Extract[p, {2}],
m3 -> Extract[p, {3}], m4 -> Extract[p, {4}]};
{opt, assign} = Minimize[thisObj, thisConstrain, var];
If[opt<0, violation++, ];
Print["opt=", opt, " perm=", p, " assign=", assign, " obj=", thisObj],
{p, Permutations[{a,b,c,d}]}
]
Print["Total number of violations =", violation];
Consider the following hypergraph with 4 vertices and 2 hyperedges each with unit weight.
We can verify the first 3 procedural minimizers.
| i | γi | fiT |
| 1 | 0 | (1,1,1,1) |
| 2 | (5-√5)/4 | (√5-1,(3-√5)/2,-1,-1) |
| 3 | (11+√5)/8 | (√5-1,-1,4-√5,-1) |
The following code verifies γ2 and γ3.
violation = 0;
Fun[list_, mask_] := Module[{ans},
l = Length[mask];
max = 0;
min = l;
Do[
max = Max[Extract[Extract[Position[list, Extract[mask, i]], 1], 1], max];
min = Min[Extract[Extract[Position[list, Extract[mask, i]], 1], 1], min];
, {i, l}];
ans = (Extract[list, max] - Extract[list, min])^2
]
constrain = {m1<=m2, m2<=m3, m3<=m4, m4==1, a+2*b+c+d==0};
var = {a,b,c,d};
Do[
thisObj = Fun[p,{b,c,d}]+(a-b)^2 - ((5-Sqrt[5])/4)*(a^2+2*b^2+c^2+d^2);
thisConstrain = constrain /. {m1 -> Extract[p , {1}], m2 -> Extract[p, {2}],
m3 -> Extract[p, {3}], m4 -> Extract[p, {4}]};
{opt, assign} = Minimize[thisObj, thisConstrain, var];
If[opt<0, violation++, ];
Print["opt=", opt, " perm=", p, " assign=", assign, " obj=", thisObj],
{p, Permutations[{a,b,c,d}]}
]
constrain = {m1<=m2, m2<=m3, m3<=m4, m4==1, a+2*b+c+d==0, (Sqrt[5]-1)*a+2*(3-Sqrt[5])/2*b-c-d==0};
var = {a,b,c,d};
Do[
thisObj = Fun[p,{b,c,d}]+(a-b)^2 - ((11+Sqrt[5])/8)*(a^2+2*b^2+c^2+d^2);
thisConstrain = constrain /. {m1 -> Extract[p , {1}], m2 -> Extract[p, {2}],
m3 -> Extract[p, {3}], m4 -> Extract[p, {4}]};
{opt, assign} = Minimize[thisObj, thisConstrain, var];
If[opt<0, violation++, ];
Print["opt=", opt, " perm=", p, " assign=", assign, " obj=", thisObj],
{p, Permutations[{a,b,c,d}]}
]
Print["Total number of violations =", violation];