In statistics, a median of a set of n numbers is the (n/2)-th smallest element of the set, that is to say, if the numbers in the set have been sorted, then the median is the element to separate the lower half subset and higher half subset of the set, so the median can be found by arranging from lowest value to highest value and picking the middle one. Note that if there are even numbers in the set, then the median is usually defined to be the average of the two middle values.
As mentioned before, sorting can be used for finding the median, however, if do so then there are some dummy operations because we only need to focus on the median one but not the whole sorted list. Since sorting n numbers takes O(n log n) operations, a better way to compute the k-th smallest of n numbers is by selection algorithm which takes only O(n) operations.
The linear algorithm of selecting the k-th smallest number was published by Blum, Floyd, Pratt, Rivest and Tarjan in their 1973 paper "Time bounds for selection", so the linear general selection algorithm is also called "BFPRT algorithm".
The idea of selection algorithm is that, as an example to find the median, based on the quickselect algorithm, if the n elements are divided into groups of several elements (usually divided into groups of five elements), for each group of five elements, the five elements can be sorted very fast, and the median of each group can be found directly, on this sublist of n/5 elements, recursively apply the selection algorithm to find the true median of n numbers. Since in the recursive step the "median of medians" is chosen to be the pivot, so selection algorithm can also be called "median of medians algorithm".
Algorithm
Assume in the set of n elements S, this SELECT algorithm returns the k-th smallest element in S
|
Time Complexity
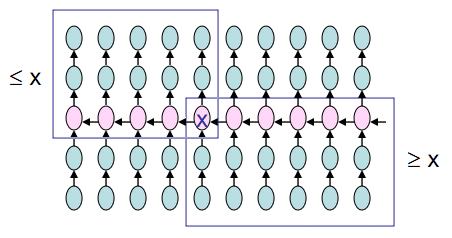
In this graph each column refers to a sorted group of 5 elements, and each element with pink colour refers to the median of the corresponding group.
Note that at least n/4 numbers >= x and at least n/4 numbers <= x, therefore at most 3n/4 numbers < x and at most 3n/4 numbers > x, i.e. |A| <= 3n/4 and |C| <= 3n/4.
In the SELECT algorithm, obviously step 1 and 4 takes O(n), and for step 2 consider sorting only 5 elements can be fast as O(n) because the number of comparisons is very small. Both step 3 and 5 apply SELECT algorithm recursively and the problem size is reduced to be n/5 and 3n/4 respectively.
By recurrence, the time complexity of selection algorithm is:
T(n) <= T(n/5) + T(3n/4) + O(n) <= O(n)