Problem:
A binary matrix is a matrix each of whose elements is either 0 or 1. Matrix A is said to be larger than matrix B if A has more entries than B. Given a binary matrix, the objective here is to find out the largest rectangle (sub-matrix) with elements being all 1’s.

Example: in above matrix, the largest all 1’s rectangle has 9 elements.

Problem solving
Suppose the matrix has m rows and n columns. The following will discuss an efficient algorithm which has time complexity O(mn). To begin with, we show some properties of all 1’s largest rectangle.
Definition

1. Bar: A bar is a line of matrix elements being all 1’s. Bar could be horizontal or vertical according to its orientation.
2. Histogram: A histogram is one horizontal bar being the base concatenating with a number of vertical bars (‘base’ means that the bottoms of vertical bars are located on the horizontal bar). We call a histogram base-k histogram if its base horizontal bar is at k-th row. Moreover, if a histogram cannot be contained within any other histogram except itself, it is a maximal histogram.

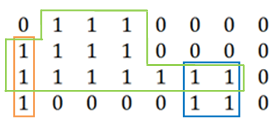
Example: maximal histograms in a matrix

Theorem 1: The largest rectangle is contained within a maximal histogram.
Proof. Note that the largest rectangle itself is a histogram. So it must be contained within some maximal histogram.

Theorem 2: For each k, any two base-k maximal histograms do not intersect.
Proof. This could be proved by contradiction. Assume that two base-k maximal histograms do intersect. Then they could be combined into a larger histogram which contains the previous two. This contradicts with the maximal property.

Theorem 2 implies that the maximal histograms could be effectively enumerated. Then by finding out the largest rectangle within each maximal histogram, we could have the overall largest rectangle.

Algorithm

A natural greedy strategy is to incrementally grow the subset by try putting in compatible activities. To use this strategy, the activities should have an order so that they can be tried one by one. Interestingly, an increasing order of finish times will lead to optimal solution (while other orderings, such as ordering in start times, will not). The algorithm is presented as follows.

Largest-Rectangle

For each row k
	For each base-k histogram H
		R = Largest-rectangle-in-histogram(H)
		If size(R) > size(maxRectangle)
			maxRectangle = R
Return maxRectangle
        

The rest is to find out the largest rectangle in a given histogram. To do this, we sweep from the histogram’s left to right and maintain a stack S: Let height(i) be the height of i-th vertical bar (for boundary case let height(0) = 0 and height(n+1) = 0, where n is the number of bars in the histogram). In i-th iteration of the sweeping we pop out all entries in S that have less height than height(i), and then push i into S, as following figure illustrates.

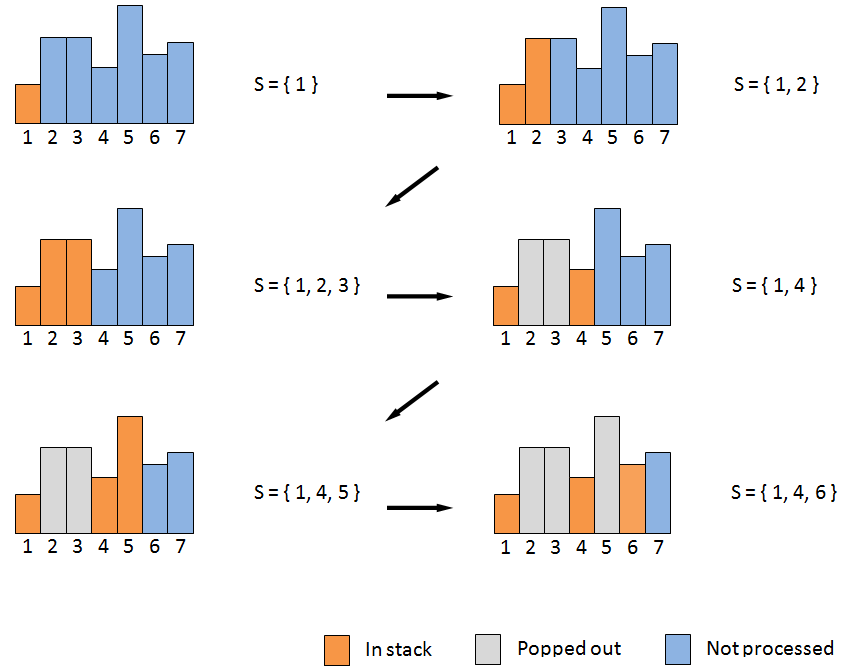
Fact 3: The heights of bars in S are non-decreasing.
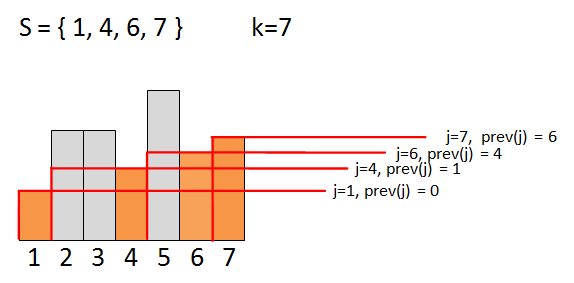
Define prev(i) as the element before i when element i is in stack S (there must be only one such element for each i). Then

Fact 4: height(j) > height(i) for any prev(i) < j < i.

The following theorem will finally lead to our Largest-rectangle-in-histogram algorithm.
Theorem 5: If k-th bar contains the right border of the largest rectangle, then (i) height(k+1) < height(k); ( ii ) size of largest rectangle  = max{ (k-prev(j)) * height(j) }, where j is each element in stack S at the start of iteration (k+1) such that height( j ) > height( k+1 ).
Proof. It is easy to see property (i), otherwise we could extend the rectangle so that it contains the (k+1)-th bar, which forms a contradiction to the right border precondition. To prove (ii), first note that the largest rectangle must contain some whole bar j (otherwise we could expand the rectangle upwards). If j is not an element in S at the start of (k+1)-th iteration, then there exists an element j ' in S such that j < j ' and height(j) > height( j ' ). In this situation j cannot be contained within a rectangle (with k-th bar as right border). And for each j in S, observe that height( i ) >= height( j ) for any prev( j ) < j <= k and height(prev( j )) < height( j ). So the largest possible rectangle containing bar j has size (k-prev(j))*height(j). Thus by enumerating j’s in S we will find out the largest rectangle in the histogram. Moreover, we will not consider j’s in S such that height(j) <= height(k+1) (i.e. j <= prev(k+1)) for similar border argument as case ( i ).

Algorithm

Largest-rectangle-in-histogram

S = { 0 }
maxSize = 0
maxRectangle = null
For k = 1 to n+1
	j = top element in S
	While height(k) < height(j) do
		Pop out the top element in S
		prev_j = top element in S
		newSize = ( k – 1 – prev_j ) * height(j)
		If newSize > maxSize
			maxSize = newSize
			update maxRectangle
		j = prev_j
	Push k into S

(We set height(0) = height(n+1) = 0 for boundary condition)

Time Complexity:
To implement Largest-rectangle, an auxiliary matrix will be prepared for quick retrieval of bar height in each maximal histogram, so the height() query only takes O(1) time. Sweeping through a histogram of length L takes O(L) amortized time considering the stack operation. The total length of every possible maximal histogram will not exceed m*n, which is the size of matrix. So the total time complexity is O(mn).

Space Complexity:
In implementation of the algorithm an auxiliary matrix of size m*n will be created. Sweeping through a histogram requires a stack of size n, which could be reused for each histogram. So the total space complexity is dominated by the auxiliary matrix and it is O(mn).

Pseudo Code

Largest-rectangle
Input: a matrix matr[1..m][1..n] valued 0 or 1.
Output: four integers (x0, y0, x0, y0) denoting the left-top 
and right-bottom corner coordinates of the largest all 1's sub-matrix

for i = 1 to m
	height[i][0] = 0
	height[i][n+1] = 0

for j = 1 to n
	height[1][i] = matr[1][j]

for i = 2 to m
	for j = 1 to n
		if matr[i][j] == 0
			height[i][j] = 0
		else
			height[i][j] = height[i-1][j] + matr[i][j]

maxSize = 0
maxRectangle = null
for i =1 to m
	S = { 0 }
	for k = 1 to n+1
		j = top(S)
		while height(k) < height(j)
			pop(S)
			prev_j = top(S)
			newSize = ( k – 1 – prev_j ) * height[i][j]
			if newSize > maxSize
				maxSize = newSize
				maxRectangle = ( i-height[i][j]+1, prev_j+1, i, k-1 )
			j = prev_j
		push(S, k)

	return maxRectangle