1. Integer Factorization in the context of Cryptography
Cryptography is an important building block of e-commerce systems. In particular, public key cryptography can be used for ensuring the confidentiality, authenticity, and integrity of information in an organization. To protect the sensitive information in an organization, encryption can be applied to conceal sensitive data so that the encrypted data is completely meaningless except to the authorized individuals with the correct decryption key. To preserve the authenticity and integrity of data, digital signature can be performed on the data such that other people can neither impersonate the correct signer nor modify the signed data without being detected.
RSA is one of the most popular public key cryptographic algorithms in used in e-commerce. Suppose Alice wants to send an encrypted message to Bob. Let the public key of Bob be <e,n> and the private key of Bob be <d,n> where n is the product of two prime numbers p and q (with ed=1 (mod (p-1)(q-1)). In this scenario, <e,n> is accessible to any one (e.g. Alice) who wants to send encrypted messages to Bob while d is kept secretly by Bob.
To encrypt a message M for Bob, Alice has to compute M’=Me (mod n). Bob can decrypt M’ by computing M’’=(Me)d=M (mod n). No one except Bob can decrypt M’ since d is only known to Bob. To calculate d from e, it is required to factor n to get p and q. With p and q, it is possible to calculate (p-1)(q-1). By reversing the key generation procedure, d can be calculated by computing e-1 (mod (p-1)(q-1)). The security of RSA depends on the difficulty in factoring n into p and q if n is sufficiently large. Therefore, the size of n should be chosen such that the time and cost for performing the factorization exceeds the value of the encrypted information.
2. Factorization Methods
Given an integer n, there
are many methods to factor it into its prime factors. Each method has its own
advantages and disadvantages.
Trial Division
The simplest method to factor n is to divide the number by small prime numbers (starting with 2, 3, 5, and so on). If the remainder of the division is zero, n is divisible by that prime number. The procedure is repeated to look for all the prime numbers less than or equal to the square root of n that can divide n.
For instance to factor the number 91, we can try to
divide 91 by 2, 3, 5, 7. The remainder when 91 is divided by 7 is 0. Therefore, 7 is one of the prime factors of 91. The other factor can be obtained by dividing 91 by 7 to get 13. Thus, the two prime factors of 91 are 7 and 13.
Trial division is simple and easy to understand. It performs reasonably well for identifying small prime factors. In some factorization packages (which will be discussed in later part of this paper), trial division is used to find prime factors of up to 9 digits. However, for large number with potentially large prime factor, it may take a very long time to try all the possible prime factors.
Pollard’s
P-1
This algorithm is proposed by John M. Pollard in 1974. This algorithm is based on Fermat’s Little Theorem which states that
a(p-1)=1 (mod p)
where a, p are integers that are relatively prime (i.e. GCD (a, p)=1).
Consider the following congruence
2x=c (mod n)
Suppose n is composed of some prime factor p, the above congruence can be written as
2x=c+kn (where k is
an integer)
2x=c+k(n/p)p
2x=c+k’p
2x=c (mod p)
Suppose x is divisible p-1, due to the Fermat’s Little Theorem, the above congruence can be simplified to
2x=1 (mod p)
2x-1=k’’p
By taking GCD(2x-1, n), we may get the factor p of n. The main question is how to select an x such that it is divisible by p-1. One way to construct x is to select a bound B and let x=B! (factorial). If (p-1) has only small factors, there is a high chance that x will be divisible by p-1.
As an example, let n=317017 and let B=5. 25!=230947 (mod n). GCD (230946,317017) =61. Hence, 61 is a factor of 317017. In this example, 5! is divisible by p-1=60 and so the prime factor 61 can be found. However, for n where there is no factor p for which p-1 has only small factors, in the worse case, this algorithm is no better than trial division. Therefore, pollard’s p-1 algorithm can be considered as special purpose algorithm to factor integers efficiently provided that n can satisfy the property discussed.
Pollard’s Rho Method
John M Pollard proposed another factorization algorithm that improves over trial division in 1975. Trial division is guaranteed to find all the factors of a number n by dividing all integers up to square root of n. For the same amount of work, it is possible to factor number up to n2 by using this method.
We consider an iteration of the form
xi=f(xi-1) (mod n)
where x0 is some random starting value between 0 and n-1 and f(x) is a polynomial with integer coefficients. One example is to choose f(x)=x2+a (where a is not equal to –2, 0). Starting from x0, we compute the sequence S=<x1, x2, x3, …> modulo n. Let d be a nontrivial divisor of n (i.e. d is a factor of n which is not equal to 1 or n itself). Since d is small compared with n, there probably exists xi, xj in S such that we have xi≡xj when modulo d but not n. Since xi-xj is divisible by d but not divisible by n, GCD (xi-xj, n)≡ GCD (kd, n) for some integer k will generate a nontrivial factor of n (which may be d or multiples of d)
However, when factoring n, the value d is unknown, we can try to calculate GCD (xi-xj, n) for all xi, xj with j<i until a non-trivial factor appears. However, it may be computationally expensive to try all possible cases. One way to reduce the complexity is to use Floyd’s method to detect cycles (modulo d) in the sequence (modulo n). The idea is to consider only the case with i=2j (where i=1, 2, 3, …).
As an example, let n=1387, x1=2, and f(x)=x2-1. We obtain x1=2, x2=3, x3=8, x4=63, x5=1194, x6=1186, etc. We calculate GCD(x2-x1, 1387)=1, GCD(x4-x2, 1387)=1, GCD(x6-x3, 1387)=19. Thus 19 is the factor of 1387. In this example, the period of cycle within the sequence is 3 and a non-trivial factor is obtained after 3 comparisons and GCD calculations.
This algorithm is more efficient than trial division and it is used by some factorization packages to find factors of between 5 and 11 digits.
Quadratic Sieve
The quadratic Sieve factoring algorithm was the most effective general purpose factoring algorithm of the 1980’s and early 1990’s. This algorithm is an improvement over the Fermat’s method and Dixon’s random square method for performing factorization. It is the method of choice for factoring integers of between 50 and 100 digits. Unlike the previous algorithm in which the running time depends mainly on the size of p and q (the factors of n), the running time of quadratic sieve and number field sieve (which will be introduced shortly) depends mainly on the size of n.
The idea of this algorithm is to find solutions where
x2=y2 (mod n)
This would imply (x-y)(x+y)=0 (mod n). By calculating GCD((x-y), n) and GCD((x+y),n), it may be possible to find a non-trivial divisor of n. In particular, when n is the product of two prime numbers p and q, the probability of finding a non-trivial factor is 2/3.
In order to find the required relation,
consider a function f(x)=x2-n. We consider the range for x with x1=
-A, x2=
+2, …, xk=
+A (where A is some suitably chosen bound). We
want to find a subset of x such that f(xi1)
f(xi2)
…f(xir) is a square number y2. Hence, the desired relation is obtained
f(xi1) f(xi2) …f(xir)=(
xi1 xi2.…xir)2 (mod n)
y2=( xi1 xi2.…xir)2 (mod n)
One way to find the xi1, xi2,…,xir such that f(xi1) f(xi2) …f(xir) is a square number is to factorize f(x1), f(x2), …, f(xk) by considering a set of chosen trial divisor {p1, p2, …, pt} (which forms the factor base F). For each f(ri), we
f(ri)=p1a1i p2a2i…ptati
If all aki are even for any k, f(ri) is a square number and we can set y2=f(ri). Otherwise, we form the exponent vector
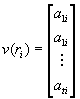
and we look for a linear combination of exponent vectors such that
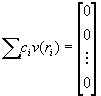(mod 2)
c1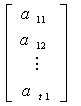
+c2
+…+ct
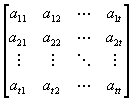
(mod 2)
(mod 2)
c1, c2, …,ct can be solved by Gaussian elimination.
The required congruence can be formed by
(mod n)
for all k in which ck=1.
For instance, to factorize n=2041, with factor base={-1, 2, 3, 5, 7}. We consider only the value of f(x) when x=43, 44, 45, 46. We have f(43)=-26*3, f(44)=-3*5*7, f(45)=-24, f(46)=3*52. We have
|
p |
-1 |
2 |
3 |
5 |
|
f(43) |
1 |
6(mod 2)=0 |
1 |
0 |
|
f(44) |
1 |
1(mod 2)=1 |
1 |
1 |
|
f(45) |
1 |
4(mod 2)=0 |
0 |
0 |
|
f(46) |
0 |
0 |
1 |
2(mod 2)=0 |
We solve the following matrix
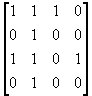
(mod 2)
(mod 2)
Thus, we can form the congruence
(43*45*46)2≡(-1)2*210*32*52=(25*3*5)2 (mod 2041)
Since GCD(2041, 43*45*46+25*3*5)=157 and GCD(2041, 43*45*46-5*3*5)=13. We can obtain the factors 157 and 13 of 2041.
Factorizing f(xi) by considering all the
divisors in the factor base is time consuming because division is one of the
most time-consuming operations in a computer. Instead of fixing f(xi)
and determining which divisor divides it, significant speed up is achieved by
fixing a prime p and determine which f(xi)
is divisible by p. Division is only
performed on the f(xi) which is actually
divisible by p. Suppose we fix a
prime p
F. Suppose f(xi)
is divisible by p. We have
f(ri) ≡0 (mod p)
ri2 –n ≡0 (mod p)
For any integer k,
f(xi+kp)= xi2 +2xikp+k2p2-n= xi2 –n ≡0
(mod p)
This implies that f(xi+kp) is also divisible by p.
With this property, we can first solve ri2 ≡n (mod p) where there exists some efficient methods for finding xi. For any xj in the range of x to be considered, we know that f(xj) will be divisible by p only if xi and xj differs by a multiple of p. In other words, we perform a “sieving” process on all f(xj) to determine the subset which is divisible by p. In fact, the sieving process can be generalized to find the subset which is divisible by pβ with β=1, 2, …, to completely factorize all f(xj). The same procedure can be repeated for all primes in the factor base.
General Number Field Sieve (GNFS)
The general number field sieve algorithm is the fastest known method for factoring large number of between 100 and 200 digits. GNFS is an improvement on quadratic sieve. The algorithm uses ideas from diverse field of mathematics such as algebraic number theory, graph theory, finite fields, and linear algebra. One of the improvements is that the polynomial being used is not only limited to quadratic, but may be cubic or even higher degree polynomials. Implementation of the number field sieve can be written such that the sieving process can take place on several computers. The result of the sieving process can be combined later. Due to the complexity involved, the details of this algorithm are outside the scope of this note.
3. Factorization attacks on RSA
In Section 1, it has been pointed out that the security of RSA depends on the difficulty of factorizing n into its constituent p and q. With the increase in the speed of computers and the improvement of factorization methods, it becomes increasingly feasible to factorize large numbers. From this perspective, choosing a longer key is essential to safeguard against attacks based on factorization. However, choosing a longer key may incur higher overhead in performing encryption and decryption. The question is given a certain amount of budget and time, what should be the length of the key that is reasonably secure without causing unnecessary performance degradation?
To keep abreast of the state of the art in factoring, RSA Security Labs launched the RSA factoring challenge to provide a testbed for factoring implementation. This provides a comparison of the effectiveness of the factoring techniques and implementations. Currently, eight challenge numbers are provided (from 576 to 2048 digits) and a prize (from $US 10,000 to $US 200,000) would be given to those who can successfully factor each number. More details about the RSA Factoring Challenges can be found in http://www.rsasecurity.com/rsalabs/challenges/.
The most recently factorized number is the RSA-155 (a number with 155 digits, which is equivalent to a 512-bit key) in august 1999 on 300 workstations and personal computers using the GNFS algorithm. The total calendar time for performing the factoring was 7.4 months (including the polynomial selection time). This result is crucial because 512-bit key is the default key length of many e-commerce applications on the Internet. Therefore, it was suggested that at least 768-bit RSA modulus should be used for personal purpose, 1024-bit RSA modulus for corporate use, and 2048-bit RSA modulus should be used for protecting extremely sensitive data.
4. Factorization Software
A list of some available factoring software is provided in this Section. They make use of some of the factorization methods discussed in this note to perform factorization. However, none of them support GNFS, which is the state of the art method for factorizing RSA modulus. In general, the performance of such factorization software is not good enough for launching factorization attack on RSA.
|
Package |
Details |
CALC
|
A calculator program for doing arbitrary precision integer arithmetic, written in ANSI C and Yacc, with a number of built-in functions for number theory, by Keith Matthews. The factorization can be performed by Pollard’s p-1 method, elliptic curve method (which is not discussed in this note), multiple polynomial quadratic sieve with less than 55 digits |
|
giantint |
Library of routines for large integer arithmetic and number theory. A factoring program is provided which first sieve over all possible prime divisor less than 2^16. Then the Pollard’s rho method is tried, then Pollard’s p-1. Elliptic curve method is then tried with increasing curve limits. |
MIRACL
|
Multiprecision Integer and Rational Arithmetic C/C++ Library. A Program is provided (factor.exe) to try brute force, Pollard’s rho, Pollard’s p-1, Pollard’s p+1, elliptic curve and multiple polynomial quadratic sieve, for windows 95/NT DOS environment The latest version factors all numbers up to 80 digits in length. |
|
Schulenberg and Associates |
Supports Trial division (with 200 digits maximum), Pollard’s rho method (with 200 digits maximum), multiple polynomial quadratic sieve (which handles “hard” input numbers of up to 100 digits). |
|
LiDIA |
C++ API and a downloadable factoring program for integer factorization (trial division, elliptic curve method, self-initializing multi-polynomial quadratic sieve with Lanczo algorithm) |
|
Factorizer |
A Windows program to find all factors of any positive integer less than 2^31 - 1, to decompose numbers into their prime constituents and to find prime numbers. (1) to get the prime decomposition of all numbers in a range of numbers, (2) to get all factors of a single number or all factors of all numbers in a range, This runs initially as a demo version which handles numbers only up to 10,000 (and does not plot histograms), but it may be activated to handle all numbers up to 2,147,483,64 after purchase. |
5. Conclusion
The security of e-commerce applications based on public key cryptography such as RSA depends on the difficulty of factorizing large integers. Given the progress in the development of new factorization methods, the increase in the computational power of personal computers, and the emergence of well-organized group of users such as distributed.net, organization should deploy public key cryptography with key length long enough to make the factorization attack difficult.
References:
- Factorization of RSA-155. http://www.rsasecurity.com/rsalabs/challenges/factoring/rsa155.html
- Factorization of 512-bit RSA key using the general number field sieve. Available at http://www.hamline.edu/~wnk/rsa/rsa.html
- ARJEN K. LENSTRA , Integer Factoring, Designs, Codes and Cryptography, 19(2000), 101–128.
- Quadratic Sieve Factoring Algorithm. http://www.math.uiuc.edu/~landquis/quadsieve.pdf
- Factoring—From MathWorld. http://mathworld.wolfram.com/topics/Factoring.html
- Finding the Prime Factors of a Number. http://pw1.netcom.com/~jrhowell/math/factor.htm
- Mathew E. Briggs, An introduction to the General Number Field Sieve, a master thesis submitted to the Faculty of the Virginia Polytechnic Institute and State University.
- Neal Koblitz , A course in number theory and Cryptography, Second Edition, Springer, 1994.
- Hans Riesel , Prime numbers and computer methods for factorization, Second Edition, Birkhauser, 1994..
- Richard A. Mollin , Fundamental Number theory with applications, CRC Press, 1997.
- Song Y. Yan , Number Theory for Computing, Second edition, Springer, 2000.
- Distributed.Net. http://www.distributed.net/