Genetic Algorithm

• Simulate Evolution Process

  • crossover

  • mutation

• Evolution through natural selection:

  • each individual tends to pass on its traits to its offspring

  • nature produces individuals with differing traits

  • the fittest individuals (those with the most favourable traits) tend to have more offspring than do those with unfavourable traits, thus driving the population as a whole towards favourable traits.

  • Over long period, variation can accumulate, producing entirely new species whose traits make them especially suited to particular ecological niches.

Example (cookies)

• There are 3 issues:

  • construction of chromosome

  • define the reproduction operations

    • mutation

    • crossover

  • define the fitness of each chromosome

• A chromosome is a representation in which

  • there is a list of elements called genes.

    
    
    

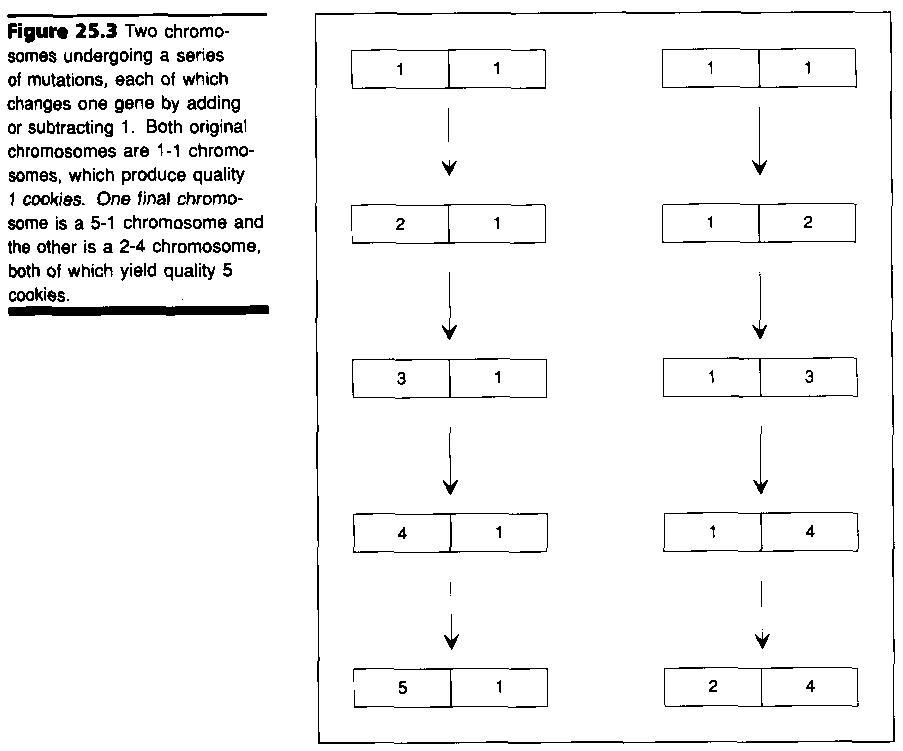
  • The chromosome determines the overall fitness manifested by some mechanism that uses the chromosome's genes as a sort of blueprint.
    
    
    

• Mutation:

• Crossover

  

• The fitness of a chromosome is the prob. that the chromosome survive to the next generation.

  e.g. q = quality score, from 1 to 9.

• In the previous example, we have:

Chromosomes	Quality	Standard Fitness
(1,4)	4	0.4
(3,1)	3	0.3
(1,2)	2	0.2
(1,1)	1	0.1

To mimic natural selection in general:

• create an initial "population" of one chromosome.

• Mutate one ore more genes in one or more of the current chromosomes, producing one new offspring for each chromosome mutated.

• Mate one or more pairs of chromosomes.

• Add the mutated and offspring chromosomes to the current population.

• Create new population by keeping the best of the current population's chromosomes, along with other chromosomes selected randomly from the current population. Bias the random selection according to assessed fitness.

Issues in the GA

1. Population Size

   • if no. too low, all chromosomes will soon have identical traits and crossover will do nothing.

   • If no. too high, problem in computation time

2. Mutation rate

   • low ¥ new traits will appear too slowly in the population

   • high ¥ each generation will be unrelated to the previous generation.

3. Mating

   • Is mating allowed?

   • How are mating pairs selected?

   • How are crossover points determined?

4. Repeated chromosome ¥ can any chromosome appear more than once in a population?

Example:

Use the following algorithm:

• starts with a single chromosome located at (1,1)

• no chromosome is permitted to appear more than once in each generation.

• A maximum of four chromosomes survive from one generation to the next.

• Each survivor is a candidate for survival to the next generation, along with any new chromosome produced.

• One gene is selected at random in each of the survivors, and is mutated at random. If the mutant is different from any candidate accumulated so far, that mutant is added to the candidates

• there is no crossover

• the chromosome with the highest score survives to the next generation

• the remaining survivors from one generation to the next are selected at random from the remaining candidates, according to the standard method for fitness computation.

• For straightforward bumplike terrain, crossover is not at all necessary

• To include crossover into the algorithm,

  • consider only the chromosomes that survived from the previous generation

  • for each chromosome, select a mate from among the other survivors. Mate selection is done at random, in keeping with the standard method for computing fitness.

  • Each mating pair is crossed in the middle, producing two crossed, offspring chromosomes. If an offspring chromosome is different from any candidate accumulated so far, that offspring chromosome is added to the candidates.

• Using crossover can overcome a moatlike function

Rank Method

• Not only offers a way of controlling the bias toward the best chromosome, but also eliminates implicit biases, introduced by unfortunate choices of the measurement scale, that might otherwise do harm.

• To select a candidate by rank method,

  • sort the n individuals by quality

  • let the probability of selecting the i-th candidate, given that the first i-1 candidates have not been selected, be p, except for the final candidate, which is selected if no previous candidate has been selected.

  • Select a candidate using the computed probabilities.

• Consider p=0.667

Chromosome	Quality	Rank	Standard fitness	Rank fitness
(1,4)	4	1	0.4	0.667
(1,3)	3	2	0.3	0.222
(1,2)	2	3	0.2	0.074
(5,2)	1	4	0.1	0.025
(7,5)	0	5	0	0.012

Diversity Principle

• it can be as good to be different as it is to be fit.

• Diversity measure:

  • e.g. Calculate the sum of the inverse squared distances between that chromosome and the other already selected chromosomes.

• Example:

Chromosome	Score	1/d2	Diversity rank	Quality rank
(1,4)	4	0.040	1	1
(3,1)	3	0.250	5	2
(1,2)	2	0.059	3	3
(1,1)	1	0.062	4	4
(7,5)	0	0.050	2	5

• To select candidate by the rank-space method:

  • sort the n individuals by quality

  • sort the n individuals by the sum of their inverse squared distances to already selected candidates

  • use the rank method, but sort on the sum of the quality rank and the diversity rank, rather than on quality rank

    

• Example (5,1) is already selected.

• Now (5,1) and (1,4) is selected. We need 2 more.

  We use diversity rank as the tie breaker.

• Finally, we get:

• The above discussed method was applied to find the optimum. We start from chromosome (1,1) and use p=0.667. 100 experiments were performed. The average number of iteration required is:

Mountain	Standard Method	Quality Rank	Rank Space
Bump	14	12	12
Moat	155	75	15

• The luckiest result: optimum obtained just after 7 iterations.