5.3 Complete Exchange Algorithms

We first derived the lower bound cost for the complete exchange operation on our abstract model - the completely connected cluster. Assuming that each node is capable to send and receive a message in one time unit, such that $(O_{s}+O_{r}+U_{r})<max(g_{s},\, g_{r})<L$. With this capability, a process can actively send and receive at the same time, thus can fully utilize the communication network. In this study, we are only focusing on the communication performance in exchanging large data block, which is the general scenario happened in most scientific and numerical computations on message passing machines. To simplify the analysis, we assume that each data block corresponds to k data packets. Therefore, the minimum amount of packets being sent and received in the complete exchange operation per process is $2k(p-1)$ packets or $2kb(p-1)$ bytes if each data packet is of size b bytes.

As the minimal time in sending or receiving a packet of size b bytes is bounded by the send gap ($g_{s}$) and receive gap ($g_{r}$), and each machine can inject or receive no more than one packet within this gap. Therefore, we deduce that the minimal time required for the complete exchange operation under such a cluster communication abstraction is

$$T_{ata} = O_{s}+max((k(p-1)-1)g_{s},(k(p-1)-1)g_{r})+L+O_{r}+U_{r}$$

$$= \left( k(p-1)-1\right) max(g_{s},\, g_{r})+O_{s}+L+O_{r}+U_{r}$$

$$= k(p-1)g+T_{w}$$ (5.1)

$$\qquad \qquad \qquad \qquad \qquad \qquad \textrm{where }T_{w}=O_{s}+L-g+O_{r}+U_{r}$$

Thus, any solution to the k-item complete exchange operation on the cluster is optimal if it takes $T_{ata}$ time units to finish the operation. Carry on with the deduction, we see that the necessary conditions to satisfy the above optimality are:

1. Each data packet must be sent directly to the target node without detour.
2. Each cluster node is actively sending and receiving the data packets without network stalling during the whole course of operation.

Condition 1 ensures that all messages appear once in the network, and therefore, minimizes the total transmission delay and messaging overhead. While with Condition 2, we ensure that no bubble exists in the network pipelines. As our performance goal is to minimize the communication time, existence of bubbles in the network pipeline means that we have to take longer time to complete the transmission. Thus, any schedule that ensures no bubble appears in the network pipelines achieves better performance.

With the assumption of complete-connected topology, links and bandwidth are sufficient but contention still exists if message transmissions are not well scheduled. In particular, any efficient algorithm in realizing the complete exchange operation must balance between synchronization and contention. This is because, due to the distributed nature of the clusters, it is difficult to impose a lock-step schedule. As most of the synchronization operations are implemented by software means, this further impedes on normal data communication and contends for network resources. In the following subsections, we review the communication schedules used by different algorithms for the complete exchange operation, and use our performance model to evaluate their performance.

5.3.1 Shift Exchange

This algorithm is the simplest way to schedule communications without node contention. It takes p-1 communication rounds, and during each round, each process sends out k items to one partner, and receives k items from another partner, which is determined by a shift pattern.

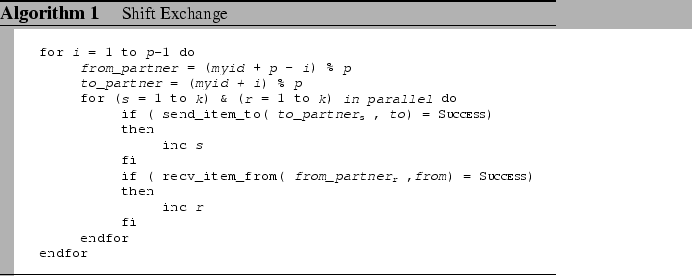
As depicted in Algorithm 1, during each round, each node uniquely maps to one sendto and recvfrom partners, thus exhibits no node contention. However, the non-stalling condition (Condition 2) is not enforced under this scheme. Although there is no explicit synchronization appeared between consecutive rounds and both send and receive operations are of non-blocking semantics, the p-1 rounds have an implicit synchronization cost that introduces bubbles to the network pipelines.

Figure 5.1: Shift Exchange pattern

For example, Figure 5.1 depicts a typical communication round. Both the send and receive channels are idle until the first byte of the first packet is being injected into the network. Similarly, after receiving the last byte of the last packet, both channels are idle until the cluster node has finished handling the last packet of this round. The predicted communication cost for this complete exchange operation is

$$T_{shift} = (p-1)(O_{s}+kg+L-g+O_{r}+U_{r})$$

$$= kg(p-1)+(p-1)T_{w}$$ (5.2)

From the cost formula, we notice that this algorithm is not optimal as there is a messaging overhead which is proportional to the number of cluster nodes, as denoted by $(p-1)T_{w}$.

5.3.2 Generalized Pairwise Exchange

In the pairwise exchange algorithm, nodes are pairing up for direct exchange in each round. Traditionally, the pairing pattern is based on the Exclusive Or (XOR) binary operation. From high-level prospective, the communication cost of the pairwise exchange algorithm coincides with that of the shift exchange as both algorithms involve the same number of communication rounds and communication load. Therefore, we can consider that $T_{pair}=T_{shift}$. We will discuss later how they may be different from an implementation view, such that their cost formulae may be different.

The major drawback of the XOR bitwise operation is the requirement of $p=2^{X}$ in order to symmetrically pairing up all the nodes. For the case with $p\neq 2^{X}$, the number of rounds becomes $2^{\left\lceil log_{2}p\right\rceil }-1$, and during each round, not all the nodes find a matching partner. The solution to the pairing problem is to find an algorithm that matches our completely-connected topology. The pairing problem can be formulated as an edge-coloring problem on any connected graph. It is defined as:

Given a graph $G=(V,E)$, with $\left\vert V\right\vert =p$ nodes connected by a set of edges (E), what is the minimum number of colors needed to color the edges of G so that no two adjacent edges are assigned the same color.

In graph theory, this is also defined as the edge-chromatic index $\chi '(G)$ of G. Thus, the solution to our schedule problem is to find an algorithm for edge-coloring the complete graph, with the edge-chromatic index represents the number of communication rounds. Due to its uniqueness, there exists a simple numerable solution comparable to the XOR bitwise operation for $p\geq 3$, and is being described and proved in [40]. By incorporated this algorithm (Algorithm 2) to the pairwise exchange scheme, we have the generalized pairwise exchange algorithm. Under this mapping scheme, the performance is only slightly deteriorated with p communication rounds for all odd cases, instead of having p-1 communication rounds for all even cases.

5.3.3 Synchronous Shuffle Exchange

The above two algorithms have a messaging overhead which is depended on the number of communication rounds. If k is small and p is large, they would perform poorly. A simple solution to this problem is by removal or reduction of this messaging overhead. We observe that the previous two schedules are arranged to avoid node contention at the message level, such that during the exchange, the whole message (k data packets) is being sent continually to the destination.

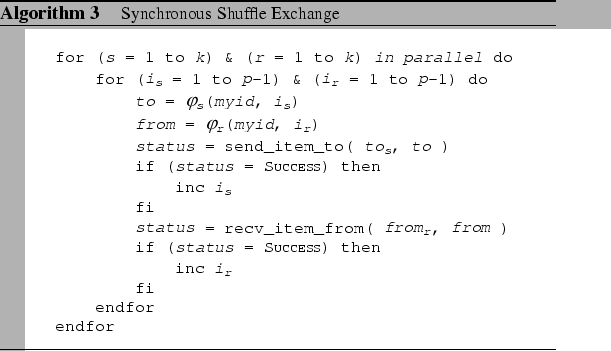
The synchronous shuffle schedule (Algorithm 3), effectively multiplexes all the p-1 messages in a single round by applying a contention-free schedule at the packet level without explicit synchronization operation. Based on that packet-level scheduling, at a particular instant $i^{j}$ (assume logically synchronized), each process is sending its $j^{th}$ packet to the process $p_{i}$ directly. And $p_{i}$ is derived from a node contention-free permutation scheme ($\varphi$), e.g. the shift pattern, the XOR pattern or the edgecolor pattern. As each process can uniquely match to different process at each packet transmission step, it guarantees no two packets are directed to the same destination at the same instant, thus no node contention. The predicted communication cost for this complete exchange operation is

$$T_{sync} = O_{s}+kg(p-1)+L-g+O_{r}+U_{r}$$

$$= k(p-1)g+T_{w}$$ (5.3)

From the cost formula, we notice that the messaging overhead is kept constant, and is not depended on p or k. In addition, this cost formula matches exactly to our optimal formula $T_{ata}$. This shows that the scheme can effectively utilize the send and receive channels by multiplexing all the messages seamlessly to a single pipeline flow without unnecessary synchronization delay.

5.3.4 Group Shuffle Exchange

If every operation is executed on schedule, and the network resources are scalable, then, the permutation scheme of the synchronous shuffle exchange could be finished in minimal time. However, in reality, logical synchronization is not enforced due to the distributed nature of the cluster system. Random delays between communication events, such as scheduling delays, could break this harmony and result in ``transient hot-spot'' in the switch. Observed that the more packets are targeting to the same output link, which are arriving from different sources at different time period, the higher chance of having conflicts even under a regular and uniform pattern. When two or more packets contend for the same output link, buffering of conflicting packets would result in routing delay. As the buffering technique within the switch has an enormous impact on the network performance, we reckon that the synchronous shuffle scheme could suffer on clusters with input-buffered switches due to the head-of-line blocking problem.

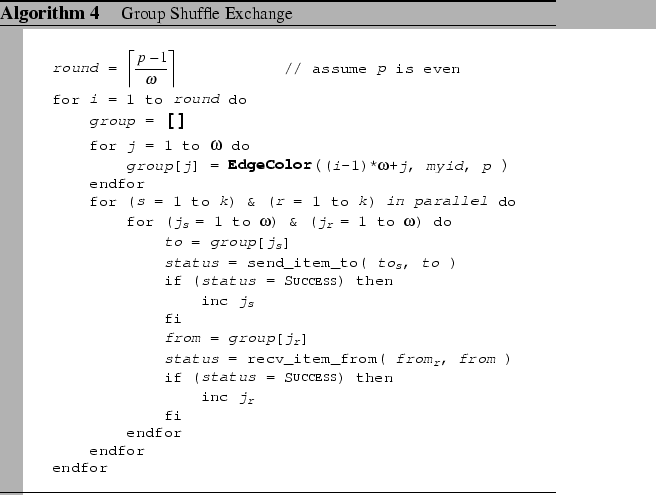
Group shuffle exchange (Algorithm 4) is a hybrid approach that combines the pairwise exchange and the synchronous shuffle exchange algorithms. The main idea is to overcome the HOL problem but still achieving comparable performance as compared to the synchronous shuffle scheme. In pure pairwise exchange scheme, packets appear in each input port are destined to a unique outgoing port in each round, thus HOL blocking does not exist even under input-buffered switch. However, in the pairwise scheme, the startup overhead is linearly proportional to the number of communication rounds, which hinders its efficiency. For the group shuffle exchange, we reduce the number of communication rounds to $\left\lceil \frac{p-1}{\omega }\right\rceil$ . In each round, a processor is performing a synchronous shuffle exchange with at most $\omega$ partners. The main idea of this scheme is to limit the degree of fan-out ($\omega$) during individual shuffle exchange phases, while keeping the number of communication rounds to a minimum.

As this algorithm comprises of more communication rounds, the startup overhead would be higher than that of the synchronous shuffle scheme but lower than the pairwise scheme. The predicted communication cost for this algorithm is, (assume $\omega$ divides p-1)

$$T_{group} = \frac{p-1}{\omega }(O_{s}+kg\omega +L-g+O_{r}+U_{r})$$

$$= kg(p-1)+\frac{p-1}{\omega }T_{w}$$ (5.4)

Table 5.1 summaries the performance characteristics of all four complete exchange schemes that we have discussed so far.

Table 5.1: Performance characteristics of different Complete Exchange schemes

	Synchronous	Group	Pairwise	Shift
Fan out degree ($\omega$)	p-1	$\omega$	1	1
No. of communication rounds	1	$\left\lceil \frac{p-1}{\omega }\right\rceil$	p-1	p-1
Pipeline stall	0	$\left\lceil \frac{p-1}{\omega }\right\rceil -1$	p-2	p-2